Display eines RaspberryPi mit Hilfe von vnc exportieren
Auf dem Raspberry Pi müssen folgende Schritte vollzogen werden:
- tight-vnc server installieren
- vncserver starten
pi@raspberrypi ~ $ apt-get install tightvncserver
pi@raspberrypi ~ $ vncserver :1 -geometry 1280x800 -depth 16 -pixelformat rgb565
Auf dem Client-PC (MacBook 2009):
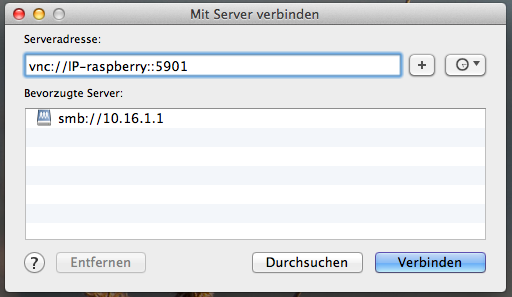
- Im Finder im Menü unter Gehe Zu den Eintrag mit Server verbinden wählen, dann muss die IP-Adresse
des RaspberryPi mit Port 5901 eintragen werden und auf Verbinden klicken.
Im Vollbildmodus sieht das exportierte Display dann so aus:
Möchte man den Export des Display stoppen, so muss auf dem RaspberryPi der Befehl eingegeben werden:
pi@raspberrypi ~ $ vncserver -kill :1